• Lecture 01：The Geometry of Linear Equations
  • Row Picture
  • Column Picture
  • Matrix Picture
  • Matrix Multiplication
  • Linear Independence

Lecture 01：The Geometry of Linear Equations

The fundamental problem of linear algebra is to solve n linear equations in n unknowns, for example:

$\begin{aligned} 2x-y\,=\,0\\ -x+2y\,=\,3 \end{aligned}$

In the first lecture, Dr. Strang show us three ways to view this problem.

Row Picture

Plot the points that satisfied each equation. The intersection of the plots (if they do intersect) is the solution of the system of above equations, which is $x\,=\,1, y\,=\,2$.

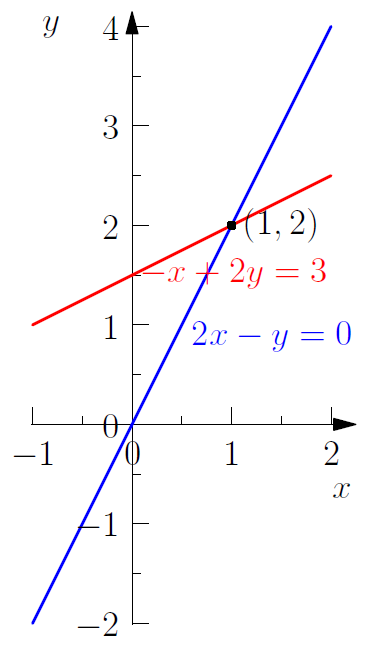
We substitute (1,2) into the original system of equations to check it’s validity:

$\begin{aligned} 2\cdot1-2\,=\,0\\ -1+2\cdot2\,=\,3 \end{aligned}$

Similarly, the solution of a three dimensional system is the common intersection of those three planes (if there does exist one).

Column Picture

In the column picture, we rewrite the system as a single equation by turning the coefficients in the column of the system into vectors:

$\begin{aligned} x \left[ \begin{array}{c} 2\\ 1 \end{array} \right] +y \left[ \begin{array}{c} -1\\ 2 \end{array} \right] = \left[ \begin{array}{c} 0\\ 3 \end{array} \right] \end{aligned}$

Given two vectors c and d and scalars x and y, the sum xc+yd is called a linear combination of c and d, which is an important concept throughout Linear Algebra.

Geometrically, we are looking for a pair of x and y which satisfies that x copies of vector $\left[\begin{array}{c}2\\-1\end{array}\right]$ added to y copies of vector $\left[\begin{array}{c}-1\\2\end{array}\right]$ equals the vector $\left[\begin{array}{c}0\\3\end{array}\right]$. As shown in Figure 2, $x=1 \;\text{and}\; y=2$ agreeing with the result we got from row picture.

In the three dimensions, the column picture requires to find a linear combination of 3-dimensional vectors that equals to the vector b.

Matrix Picture

Rewrite the system of equations as a single equation by using matrices and vectors:

$\begin{aligned} \left[ \begin{array}{cc} 2 & -1\\ -1 & 2\\ \end{array} \right] \left[ \begin{array}{c} x\\ y \end{array} \right] =\left[ \begin{array}{c} 0\\ 3 \end{array} \right] \end{aligned}$

The matrix $\left[\begin{array}{cc}2&-1\\-1&2\end{array}\right]$ is called the coefficient matrix. The vector $\bold{x}=\left[\begin{array}{c}x\\y\end{array}\right]$ is the vector of unknowns. The value on the right hand side of the equations form the vector b:

$A\bold{x}=\bold{b}$

The three dimensional matrix picture is similar to the two dimensional one, except that the vectors and matrices increase in size.

Matrix Multiplication

How do we multiply a matrix A by a vector x?

$\left[ \begin{array}{cc} 2&5\\ 1&3 \end{array} \right] \left[ \begin{array}{c} 1\\2 \end{array} \right] =\;?$

The method Dr. Strang suggests is to think of the entries of x as the coefficients of a linear combination of the column vectors of the matrix:

$\left[ \begin{array}{cc} 2&5\\1&3 \end{array} \right] \left[ \begin{array}{c} 1\\2 \end{array} \right] =1\left[ \begin{array}{c} 2\\1 \end{array} \right] +2\left[ \begin{array}{c} 5\\3 \end{array} \right] =\left[ \begin{array}{c} 12\\7 \end{array} \right]$

The technique shows that Ax is a linear combination of the columns of A.

Also, you can calculate the product Ax by taking dot product of each row of A with the vector x:

$\left[ \begin{array}{cc} 2&5\\1&3 \end{array} \right] \left[ \begin{array}{c} 1\\2 \end{array} \right] =\left[ \begin{array}{c} 2\cdot1+5\cdot2\\1\cdot1+3\cdot2 \end{array} \right] =\left[ \begin{array}{c} 12\\7 \end{array} \right]$

Linear Independence

In the column and matrix pictures, the right hand side of the equation is a vector b. Given a matrix A, if we can solve:

$A\bold{x}=\bold{b}$

for every possible b, we say that A is an inversible matrix, which means that the linear combinations of the column vectors fill the xy-plane (in two dimensional case). Otherwise, we say that A is a singular matrix, whose column vectors are linear dependent, or in other words, all linear combinations of those vectors lie on a point or line (in two dimensional case). In such case, the combinations don’t fill the whole space.